前回はデータ分析とデータ整理の違いについて解説した。
今回は実際にデータ分析するにはどういったアプローチが必要かについて。
データ分析はたいていの場合、何か目的があって始めるはず。
その目的を考えず、ただデータを集めたり眺めていても何もわからない。
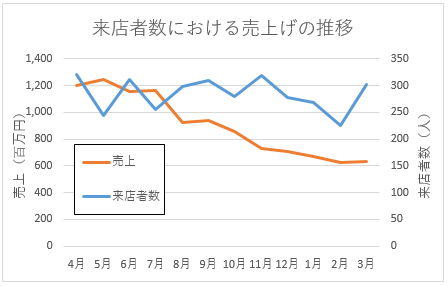
一般的な会社がよく陥っているのは「売上げや利益の推移や前年比をみながら推理している」ケース。
前回も説明したが、売上推移からは売上げの推移しかわからないし、
前年比は前年と比較してどうなのかしかわからない。
では、実際のところどうすればよいか?
データ整理から抜け出しデータ分析にするためのアプローチ
データ分析では次の順番でアプローチしていく。
| 何のために? | > | 目的、課題を定義する |
| 何を見るのか? | > | 見るべきデータと指標を決定する |
| どうみるのか? | > | 多面的にデータを捉える |
| なぜそうなのか? | > | 理由、原因を数値化して捉える |
順番に解説していこう。
「何のために?」を明確にする(目的、課題を定義する)
よくあるのは目的がはっきりしないまま分析を始めてしまうケース。
これをちゃんとやっておかないと、すぐに迷走してしまう。
課題を定義する時のポイントは、
課題が明確になっており、次のアクションが具体的になっているか?
悪い例)社員の健康に問題がある
良い例)社員の病気による欠勤が増加している事が問題である
「悪い例」では健康の何が問題なのかが曖昧なまま。
体調が悪い人がいてパフォーマンスが悪化している事が問題なのか、
遅刻が増えている事が問題なのか?
一方「良い例」では「欠勤が増加している事」が問題だとわかる。
課題が具体的になったら、その状態を把握、評価する軸を決める。
上記の「割る異例」のように課題定義が曖昧だと、何を軸に評価していいかわからない。
「良い例」のように課題が具体的になっていれば、
病気による欠勤数を測定すればいいことがわかる。
「何を見るのか?」を決める(見るべきデータと指標を決定する)
先の例であれば、
・1日辺りの欠勤した人数 ・1人辺りの欠勤数 etc...
ここまで決めて、初めてデータを見る。
これをしておかないと他のデータに目移りしてしまったり、
限られた情報の中から無理やり答えを導こうとしてしまい、
正しい結論に到達できない。
「何をみるのか?」がいきなりはわからない場合
課題のポイントを特定する
全体的なデータを見ていると、傾向はつかめても原因まではわからない。
その場合、データを分解して細かくしていき、
課題を引き起こしているポイントを絞り込んでいく。
その際、闇雲に分解するのではなく、分解した結果に差が出てくるように分解していく。
例)利益が下がっている
売上げがさがっているのか?コストが下がっているのか?
それぞれ比較し、差の有無を確認する。
差が大きい切り口をさらに分解する。
(売上げなら店舗ごと、商品ごと、コストなら経費と原価等)
ここでやりがちな失敗
「差を見つけた!」を結論にしてしまいがち。
そもそも差を見つけることが目的ではない。
なぜ差が生まれたのか?そこから次のアクションを考える。
「どう見るのか?」
ただデータを眺めていてもうまく比較ができない。
同じデータでも多面的に見ることで新たな比較軸が出てくる。
データを多面的に見る具体的なポイントは、以下の3つの観点で比較してみること。
- 大きさ(比率)
- 推移
- バラつき
金額の大小、規模の大小、割合の大小
その値は徐々に増加しているのか?減少しているのか?
その値は平均的なのか?レアケースなのか?
平均値からでは見えないこと
よくやってしまうのが、平均で傾向を見ようとするがケース。
平均値は簡単に算出でき便利な手法だが、
結果的に見えなくなる部分がある事は理解しておく必要がある。
例)2店舗でアンケートをとった結果、僅差でB店舗のほうが評価が高い。
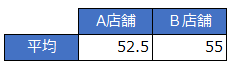
でも、実はこの2店のアンケート結果にはかなり差がある。
1)来店者アンケートで、半分以上の回答が90点以上だったが、一部低い点だった。
2)来店者アンケートで、ほとんどの人が55点だった。
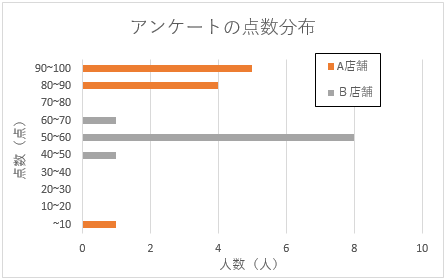
この場合、実際の評判はA店の方がよいと予想される。
このように、平均点を見ていると見えない部分がある。
では、どうするか?
バラつきを数値化する(標準偏差)
平均値で見えないデータのバラつきを数値化したものが「標準偏差」。
標準偏差はExcelで簡単に求められるので、細かい説明は省略。
標準偏差の求め方
標準偏差は値が大きければバラつきが多く、値が小さければバラつきが少ない。
先ほどのアンケート結果では以下のようになる。
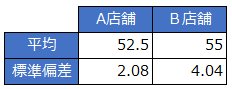
ここで注意したいのは、
「バラつきが大きい=良い」というわけではないと言うこと。
比較するのが売上げなら、「標準偏差が大きい=安定していない」ともいえる。
逆におなじ売上げの標準偏差でも、
「バラつきが大きい=売上げを伸ばす余地がある」と捉えることもできる。
値をどう解釈するかは別の問題。
標準偏差はあくまで、「バラつきを数値化したもの」と考える。
標準偏差からでは見えないこと
テストの点数など全員が同じ指標であれば、標準偏差で比較できるが
元々の規模が違うと単純に比較できない。
以下のケースでは、標準偏差は同じだがバラつきが与えるインパクトはB店舗のほうが大きい。
A店舗:売上平均 9,000万円、 標準偏差:100万円
B店舗:売上平均 500万円、 標準偏差:100万円
※月の売上平均が9000万円のA店舗で100万円の売上減は誤差の範囲と言えるが
月売上平均が500万円のB店舗で100万円の売上減は致命傷かもしれない。
そこで、標準偏差を変動係数に変換することでバラつきを比較する。
変動係数は以下の式で求める。
- 変動係数=標準偏差/平均
先ほどの例だと以下のようになる。
A店舗:売上平均 9,000万円、 標準偏差:100万円、 変動係数:0.01
B店舗:売上平均 500万円、 標準偏差:100万円、 変動係数:0.2
これで、バラつきを相対的に比較できるようになった。
バラつきだけにとらわれない
標準偏差や変動係数をみていると、その値だけにとらわれがちになる。
例えば以下のケースではA店舗よりC店舗の方が変動係数は小さい。
A店舗:売上平均 9,000万円、 標準偏差:100万円、 変動係数:0.01
C店舗:売上平均 0万円、 標準偏差: 0円、 変動係数:0.00
※毎月の売上は0円だがバラつきはないので、変動係数は0(バラつきがない)となる。
これは極端な例だが、標準偏差や変動係数だけにとらわれると間違った結果になってしまう典型。
バラつきと平均をうまく組み合わせて、結論を導くことが重要となる。
さて、ようやく分析するものができたので、
実際の分析に入るが、長くなってきたので続きは次回。

コメント